日本大百科全書（ニッポニカ）

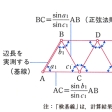
地上の互いに見通せる3点を選んで三角形をつくり、その1辺の長さおよび2夾角（きょうかく）を測定して、三角法により他の2辺の長さや頂点の位置を求める古典的な測量法。三角形を多数接続させて広い範囲の測量を能率よく、かつ精度よく行える。このような三角形の集合を三角網というが、鎖状につないだ場合は三角鎖（さ）といい、広大な地域の骨組みとしての三角測量の場合に使われる。
　三角網あるいは三角鎖の測量では少なくとも1辺の長さを実測しておかねばならない。これを基線といい、この長さの測定には25メートルのインバール（温度によって伸び縮みしにくい合金）製の尺が用いられたが、1970年代には精密な電磁波測距儀により三角形の辺長が直接測定できるようになった。また少なくとも1点の地球上の位置と1方向の方位とは与えておかなければならず、これは天文測量により決定される。
　精密な三角測量では3内角を観測してその和を求め、観測誤差の点検調整を行うが、1辺が数十キロメートルに及ぶ地球上の三角形は球面三角となり、3内角の和は180度よりは多少大きくなる。これを球過量あるいは球面過剰といい、三角形の面積が100平方キロメートル（1辺の長さ約14キロメートル）の場合の球過量は約0.5秒、1辺の長さ約40キロメートルでは約8秒となる。
　三角網には一等、二等、三等、四等などの等級があり、しだいに細かい網をつくって上級の網のすきまを埋めていく。これらの網の調整計算には膨大な計算量が必要なので、適当な大きさの三角網群にくぎってそれぞれ別個に計算を行っていたが、1970年代にはコンピュータの利用により、日本全国をいちどきに調整計算することができるようになり、再計算もされた。また三角網が大きくなると、観測誤差が累積して網にねじれが生じるので、所々の三角点で天文測量を実施して、このねじれを規制する。この点をラプラス点という。1970年代以降、精密な電磁波測距と電子計算機による全国の厳密調整計算による再測も行われたが、1990年代以降はGPS衛星を用いた測量により三角網の再測が行われている。
［尾崎幸男・辻　宏道］