日本大百科全書（ニッポニカ）

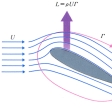
粘性のない流体の一様な流れの中に、任意の断面形の柱状物体を流れに直角に置くとき、物体には流れに直角方向の力、すなわち揚力が働く。その大きさは、物体の軸方向の単位長さ当りL＝ρUΓであるという定理。ただし、ρは流体の密度、Uは一様流の速度、Γは物体の周りの循環である。
　この定理は、飛行機の翼の理論で基礎的な重要性をもっている。たとえば、一様な流れに対して翼を傾けておくと、翼を回るような流れが誘発される。その大きさを示す量が流体力学で循環とよばれるものである。翼の傾きを増すほど循環Γは大きくなる。またΓは流速Uに比例する。したがって、揚力は流体の密度に比例し、流速の2乗に比例し、かつ翼の傾きが大きいほど大きい。なお、円柱を回転させながら流れにさらすときにも、円柱の周りに循環ができるので、円柱には揚力が働く。この定理は、柱状物体を過ぎる二次元的な流れについて述べるものであるが、球のような三次元的な物体についても定性的に成り立つ。回転を与えた野球のボールがカーブする現象はこれによって説明される。
［今井　功］